Resampling, Smoothing and Interest points of curves (via CSS) in OpenCV [w/ code]

I’m so glad to be back to work on a graphics project (of which you will probably hear later), because it takes me back to reading papers and implementing work by talented people. I want share a little bit of utilities I’ve developed for working with 2D curves in OpenCV.

Smooth operator

So I’ve been implementing a paper called “Affine-invariant Shape Matching and Recognition Under Partial
Occlusion” by Mai, Chang and Hung from 2010 (Here), that is using the CSS Image (Curvature Scale Space, rather an old concept, developed by Mukhtarian in the mid-1990s) to extract affine-invariant points on curves. The work is rather simple and the paper is short, but nevertheless powerful.
In the process of computing the CSS Image, once must smooth the curve with gaussian kernels of varying sizes, and this I’d like to show you.

The implementation is simple:

/* 1st and 2nd derivative of 1D gaussian
 */
void getGaussianDerivs(double sigma, int M, vector<double>& gaussian, vector<double>& dg, vector<double>& d2g) {
	int L = (M - 1) / 2;
	double sigma_sq = sigma * sigma;
	double sigma_quad = sigma_sq*sigma_sq;
	dg.resize(M); d2g.resize(M); gaussian.resize(M);
	Mat_<double> g = getGaussianKernel(M, sigma, CV_64F);
	for (double i = -L; i < L+1.0; i += 1.0) {
		int idx = (int)(i+L);
		gaussian[idx] = g(idx);
		// from http://www.cedar.buffalo.edu/~srihari/CSE555/Normal2.pdf
		dg[idx] = (-i/sigma_sq) * g(idx);
		d2g[idx] = (-sigma_sq + i*i)/sigma_quad * g(idx);
	}
}
/* 1st and 2nd derivative of smoothed curve point */
void getdX(vector<double> x,
		   int n,
		   double sigma,
		   double& gx,
		   double& dgx,
		   double& d2gx,
		   vector<double> g,
		   vector<double> dg,
		   vector<double> d2g,
		   bool isOpen = false)
{
	int L = (g.size() - 1) / 2;
	gx = dgx = d2gx = 0.0;
//	cout << "Point " << n << ": ";
	for (int k = -L; k < L+1; k++) {
		double x_n_k;
		if (n-k < 0) {
			if (isOpen) {
				//open curve - mirror values on border
				x_n_k = x[-(n-k)];
			} else {
				//closed curve - take values from end of curve
				x_n_k = x[x.size()+(n-k)];
			}
		} else if(n-k > x.size()-1) {
			if (isOpen) {
				//mirror value on border
				x_n_k = x[n+k];
			} else {
				x_n_k = x[(n-k)-(x.size())];
			}
		} else {
//			cout << n-k;
			x_n_k = x[n-k];
		}
//		cout << "* g[" << g[k + L] << "], ";
		gx += x_n_k * g[k + L]; //gaussians go [0 -> M-1]
		dgx += x_n_k * dg[k + L];
		d2gx += x_n_k * d2g[k + L];
	}
//	cout << endl;
}
/* 0th, 1st and 2nd derivatives of whole smoothed curve */
void getdXcurve(vector<double> x,
				double sigma,
				vector<double>& gx,
				vector<double>& dx,
				vector<double>& d2x,
				vector<double> g,
				vector<double> dg,
				vector<double> d2g,
				bool isOpen = false)
{
	gx.resize(x.size());
	dx.resize(x.size());
	d2x.resize(x.size());
	for (int i=0; i<x.size(); i++) {
		double gausx,dgx,d2gx; getdX(x,i,sigma,gausx,dgx,d2gx,g,dg,d2g,isOpen);
		gx[i] = gausx;
		dx[i] = dgx;
		d2x[i] = d2gx;
	}
}

The smoothing runs on each of the curves dimensions (i.e. x and y) separately, so I create little helper functions:

template<typename T, typename V>
void PolyLineSplit(const vector<Point_<T> >& pl,vector<V>& contourx, vector<V>& contoury) {
	contourx.resize(pl.size());
	contoury.resize(pl.size());
	for (int j=0; j<pl.size(); j++)
	{
		contourx[j] = (V)(pl[j].x);
		contoury[j] = (V)(pl[j].y);
	}
}
template<typename T, typename V>
void PolyLineMerge(vector<Point_<T> >& pl, const vector<V>& contourx, const vector<V>& contoury) {
	assert(contourx.size()==contoury.size());
	pl.resize(contourx.size());
	for (int j=0; j<contourx.size(); j++) {
		pl[j].x = (T)(contourx[j]);
		pl[j].y = (T)(contoury[j]);
	}
}

They also convert to different types if needed.
Smoothing is easy:

vector<Point> curve = ...;
double sigma = 3.0;
int M = round((10.0*sigma+1.0) / 2.0) * 2 - 1;
assert(M % 2 == 1); //M is an odd number
//create kernels
vector<double> g,dg,d2g; getGaussianDerivs(sigma,M,g,dg,d2g);
vector<double> curvex,curvey,smoothx,smoothy;
PolyLineSplit(curve,curvex,curvey);
vector<double> X,XX,Y,YY;
getdXcurve(curvex,sigma,smoothx,X,XX,g,dg,d2g,isOpen);
getdXcurve(curvey,sigma,smoothy,Y,YY,g,dg,d2g,isOpen);
PolyLineMerge(curve,smoothx,smoothy);

Resampling

I implemented my own resampling code, where I sample points on the curve keeping the same regular distance between them. To get the regular distance I simply take the complete length of the original curve and divide by the number of desired points.

The implementation is again quite simple:

void ResampleCurve(const vector<double>& curvex, const vector<double>& curvey,
				   vector<double>& resampleX, vector<double>& resampleY,
				   int N,
				   bool isOpen
				   ) {
	assert(curvex.size()>0 && curvey.size()>0 && curvex.size()==curvey.size());
	vector<Point2d> resamplepl(N); resamplepl[0].x = curvex[0]; resamplepl[0].y = curvey[0];
	vector<Point2i> pl; PolyLineMerge(pl,curvex,curvey);
	double pl_length = arcLength(pl, false);
	double resample_size = pl_length / (double)N;
	int curr = 0;
	double dist = 0.0;
	for (int i=1; i<N; ) {
		assert(curr < pl.size() - 1);
		double last_dist = norm(pl[curr] - pl[curr+1]);
		dist += last_dist;
//		cout << curr << " and " << curr+1 << "\t\t" << last_dist << " ("<<dist<<")"<<endl;
		if (dist >= resample_size) {
			//put a point on line
			double _d = last_dist - (dist-resample_size);
			Point2d cp(pl[curr].x,pl[curr].y),cp1(pl[curr+1].x,pl[curr+1].y);
			Point2d dirv = cp1-cp; dirv = dirv * (1.0 / norm(dirv));
//			cout << "point " << i << " between " << curr << " and " << curr+1 << " remaining " << dist << endl;
			assert(i < resamplepl.size());
			resamplepl[i] = cp + dirv * _d;
			i++;
			dist = last_dist - _d; //remaining dist
			//if remaining dist to next point needs more sampling... (within some epsilon)
			while (dist - resample_size > 1e-3) {
//				cout << "point " << i << " between " << curr << " and " << curr+1 << " remaining " << dist << endl;
				assert(i < resamplepl.size());
				resamplepl[i] = resamplepl[i-1] + dirv * resample_size;
				dist -= resample_size;
				i++;
			}
		}
		curr++;
	}
	PolyLineSplit(resamplepl,resampleX,resampleY);
}

Essentially I just traverse the original curve, advancing in a regular pace (resample_size) and adding new vertices as long as there is space to so on the current edge. If space to add more vertices on the edge – I move to the next edge and add more vertices there.

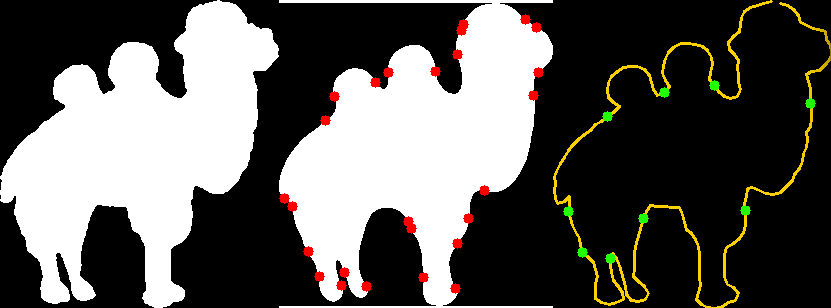
Curvature Scale Space

The core idea of the CSS image (as shown perhaps best by Mokhtarian and Abbassi in their 2002 paper) is to smooth the curve by ever increasing gaussian kernels and looking at zero crossings of the 2nd derivative. When you’re smoothing the curve you will loose the noise, and be left with only the biggest changes in curvature, and a zero-crossing on the 2nd derivative will indicate a big change in curvature. The invariant points across the different sizes of the gaussian kernel – are the interest points of the curve (sometimes referred to as “affine invariant”).

/* compute curvature of curve after gaussian smoothing
 from "Shape similarity retrieval under affine transforms", Mokhtarian & Abbasi 2002
 curvex - x position of points
 curvey - y position of points
 kappa - curvature coeff for each point
 sigma - gaussian sigma
 */
void ComputeCurveCSS(const vector<double>& curvex,
					 const vector<double>& curvey,
					 vector<double>& kappa,
					 vector<double>& smoothX, vector<double>& smoothY,
					 double sigma,
					 bool isOpen
					 )
{
	int M = round((10.0*sigma+1.0) / 2.0) * 2 - 1;
	assert(M % 2 == 1); //M is an odd number
	vector<double> g,dg,d2g; getGaussianDerivs(sigma,M,g,dg,d2g);
	vector<double> X,XX,Y,YY;
	getdXcurve(curvex,sigma,smoothX,X,XX,g,dg,d2g,isOpen);
	getdXcurve(curvey,sigma,smoothY,Y,YY,g,dg,d2g,isOpen);
	kappa.resize(curvex.size());
	for (int i=0; i<curvex.size(); i++) {
		// Mokhtarian 02' eqn (4)
		kappa[i] = (X[i]*YY[i] - XX[i]*Y[i]) / pow(X[i]*X[i] + Y[i]*Y[i], 1.5);
	}
}
/* find zero crossings on curvature */
vector<int> FindCSSInterestPoints(const vector<double>& kappa) {
	vector<int> crossings;
	for (int i=0; i<kappa.size()-1; i++) {
		if ((kappa[i] < 0 && kappa[i+1] > 0) || kappa[i] > 0 && kappa[i+1] < 0) {
			crossings.push_back(i);
		}
	}
	return crossings;
}

The evolution of the curve (iterating through many levels of the gaussian kernel) looks like the following:

Code

Grab the code: http://web.media.mit.edu/~roys/src/CurveCSS.zip
(if the hosting dies – let me know)
Thanks for joining in
Roy.