Shape manipulation with Moving Least Squares for curves [w/ code]

Hello,
I wanna share some code I’ve been working on lately that implements smooth shape manipulation using Moving Least Squares. More specifically, the excellent simple and powerful method by Schaefer et al. from Texas A&M and Rice universities (great paper). The method was written for image deformation but very straightforward modifications made it work perfectly for 2D shapes and open curves.
Let’s get down to business

Affine, similarity and rigid deformations

The beauty with Schefer’s method is that it simple to implement, presents powerful results and is blazing-fast because of the optimizations they suggest in the paper (decomposing the math to allow pre-computing as much as possible). Initially they show three methods for deformation: Affine, Similarity and Rigid.
Affine deformation means that, locally, affected points could undergo a complete affine transformation, meaning: Rotation, Translation, non uniform Scale, Shear and Squeeze. While it is still cool, it can unrealistically distort the shapes.

See how in extreme stretch the top fin and mouth of the fish are distorted.
Similarity transformations allow only Rotation, Translation and uniform Scale, which makes the deformation more appealing, but it does tend to enlarge parts on extreme stretch:

Finally, Rigid transformation only allow local Rotation and Translation, keeping the deformed shape more rigid:

Using the code

Everything is encapsulated in the SchaeferMLS template class:

template<typename T>
class SchaeferMLS {
public:
	void Init(const vector<Point_<T> >& curve, const vector<int>& control_idx) {...}
	void UpdateAffine() {...}
	void UpdateSimilarity() {...}
	void UpdateRigid() {...}
	const vector<Point_<T> >& GetControlPts() { ...}
	vector<Point_<T> >& GetDeformedControlPts() { ...}
	void Draw(Mat& img) {...}
};

I’ve written a small app to show simple usage with the different deformation types, it’s fairly simple to follow.
But the gist is:

//Read curve
vector<Point> a;
GetCurveForImage(imread("a_slihouette.png", a, false);
//Convert to Point_<double> - optional
vector<Point2d> a_p2d, a_p2d_smoothed;
ConvertCurve(a, a_p2d);
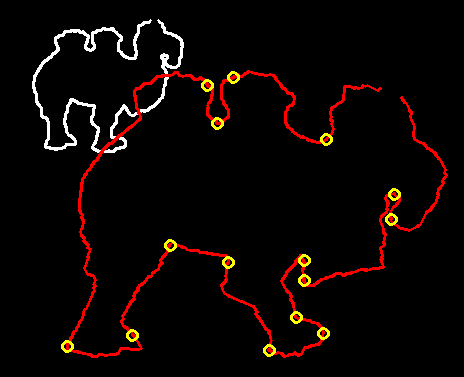
//Get curvature extrema points
vector<pair<char,int> > stringrep = CurvatureExtrema(a_p2d, a_p2d_smoothed,0.05,4.0);
//Get extrema as control points
vector<int> control_pts;
for(int i=0;i<stringrep.size();i++) {
	control_pts.push_back(stringrep[i].second);
}
smls.Init(a_p2d, control_pts);
smls.UpdateRigid();
Mat visualized_curve(500,500,CV_8UC3);
smls.Draw(visualized_curve);
namedWindow("MLS");
//Implement the onMouse function (or take from repo) to reflect changes in control points
setMouseCallback("MLS", onMouse, NULL);
imshow("MLS", visualized_curve);
waitKey();

You can grab the code at github: https://github.com/royshil/CurveDeformationMLS
Thanks for tuning in!
Roy.