
Just sharing some code and ideas for matching 2D curves. I was working for a while on matching 2D curves to discover shapes in images, but it didn’t work out, what did succeed is this 2D curve matcher that seems to be very robust for certain applications. It’s based on ideas from the Heat Kernel Signature and the CSS Image (that I introduced in my latest post), all around inspecting curves under different level of smoothing.
Principle
The idea is simple, take the curve and build a “Signature Database” for it, which then you compare to another DB.
The database is essentially every possible sub-curve of the curve, under every possible offset, all normalized to the same length.
This also makes this method quite robust to occlusions! (where only part of the target curve is available)

The matching is done over the curvature of (a smoothed version of) the curve, the 2nd derivative, which was nicely explained in this paper by Mokhtarian in 2002.
Working with the functions
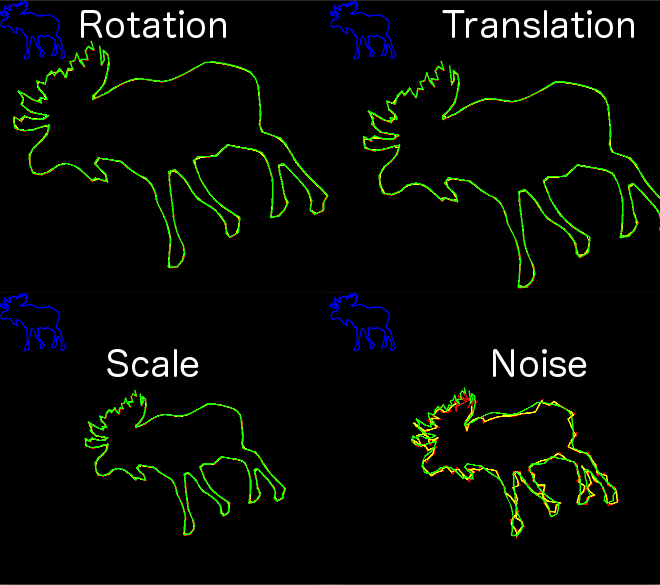
I created a sample app that takes in a curve (binary image with contour extracted), transforms it and then tries to find a match with the original.
But the central function is
template void CompareCurvesUsingSignatureDB(const vector<Point_ >& a, const vector<Point_ >& b, int& a_len, int& a_off, int& b_len, int& b_off, double& score );
It takes in any type of curve (Point, Point2f, Point2d) and returns the length and offset inside each curve of the sub-curves that best match.
You can then find a rigid transformation easily by
//assume you have vector a,b; from before //Get matched subsets of curves vector a_subset(a.begin() + a_off, a.begin() + a_off + a_len); vector b_subset(b.begin() + b_off, b.begin() + b_off + b_len); //Normalize to equal length ResampleCurve(a_subset, a_subset, 200, true); ResampleCurve(b_subset, b_subset, 200, true); //Find rigid transformation Mat trans = Find2DRigidTransform(a_subset, b_subset); vector a_trans; cv::transform(a_subset,a_trans,trans);
Code and salutations
Get the code at the github repo
Enjoy!
Roy.
7 replies on “2D curve matching in OpenCV [w/ code]”
If you’re studying curve matching, then you’ll probably find this thesis interesting: http://tel.archives-ouvertes.fr/tel-00133648 (it’s in English, don’t be afraid by the title). If I remember correctly my reading, it does actually contain a method for robust piecewise curve matching.
I remember implementing Mokhtarian’s CSS for a Master course several years ago, occlusions were indeed a real difficulty for this kind of silhouette-based recognition algorithm.
Keep on the great blogging, and thanks for all the posts !
Dear Roy,
I am interested to know how the matching function works. I downloaded the code folder and I found out CLSignatureMatching.h header is not the folder. May you please upload this header file which is used for CompareSignaturesGPU.
Thanks for your post
When the curve rotates an angle,the curvature cannot keep the same as origin for the same point. And, the curvatures for a closed circle shape vary largely.
Drear sir,
I think you did a really good job here, i would like to ask if you have a working example of this function? If you do, would you be so generous to share it with me, i’ve been trying to make it work, but without success.
Thanks for your inspiration!
From Czech Republic,
Stepan
Sorry if I bother you with my programming problem, but i tried your code and independently by the image I load i continue to have the following error:
Assertion failed: (curvex.size()>0 && curvey.size()>0 && curvex.size()==curvey.size()), function ResampleCurve
I discover that curvex and curvey are empty because “GetCurveForImage” exit without generating any curve.
I think the problem is here
if (upperCurve.size() <= 50) {
return;
}
but i can't understand why.
Maybe you can enlighten me.
Thanks,
Riccardo
[…] I found this code that does exactly what I want: https://www.morethantechnical.com/2012/12/27/2d-curve-matching-in-opencv-w-code/ but is in […]
Hi, is it normal that compareDB takes 20 seconds to finish?